Page 1 of 1
x' and t
Posted: Wed Jun 26, 2013 11:21 am
by A Random Player
If I know x' and t (in a
Minkowski diagram), or x and t', how do I find x and t?
(Making a simple Minkowski diagram drawer.)
Edit: Without solving a system of equations.
Re: x' and t
Posted: Thu Jun 27, 2013 1:24 am
by testtubegames
Without solving a system of equations, eh? Well, you'll need to deal with the Lorentz Transformations to be sure. But they aren't too tough (haha... I make myself laugh...). At least what you're looking to do shouldn't be too hard.
Lorentz Transformations
If you check out the equations, using the first one you come across (t' = ...), you'll see that three coordinates are represented. So if you want to find t, start with the equation for t', then rearrange it to find t as a function of t' and x.
Does this make sense / fit what you're trying to do?
Re: x' and t
Posted: Thu Jun 27, 2013 11:18 am
by A Random Player
testtubegames wrote:Without solving a system of equations, eh? Well, you'll need to deal with the Lorentz Transformations to be sure. But they aren't too tough (haha... I make myself laugh...). At least what you're looking to do shouldn't be too hard.
Lorentz Transformations
If you check out the equations, using the first one you come across (t' = ...), you'll see that three coordinates are represented. So if you want to find t, start with the equation for t', then rearrange it to find t as a function of t' and x.
Does this make sense / fit what you're trying to do?
Looks right!

It's been so long since I needed simple Algebra

Re: x' and t
Posted: Thu Jun 27, 2013 3:20 pm
by testtubegames
A Random Player wrote:
Looks right!

It's been so long since I needed simple Algebra

Haha, sure. What exactly are you making with it? (you've got me intrigued)
Re: x' and t
Posted: Thu Jun 27, 2013 3:32 pm
by A Random Player
testtubegames wrote:A Random Player wrote:
Looks right!

It's been so long since I needed simple Algebra

Haha, sure. What exactly are you making with it? (you've got me intrigued)
This:
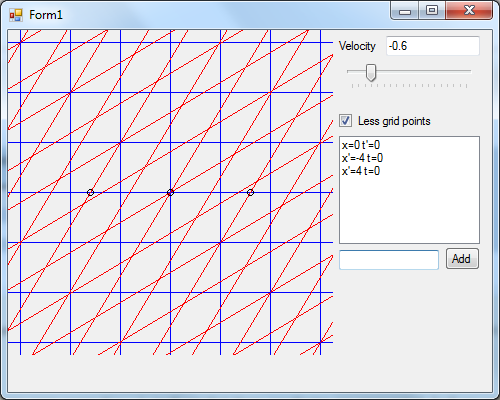
- Length contraction, as example.
- Minkowski screenshot.png (40 KiB) Viewed 23782 times
I'm running into divide by 0 errors on x and x', and t and t', but that's to be expected.
Re: x' and t
Posted: Fri Jun 28, 2013 10:57 pm
by testtubegames
Neat! At first glance, it looks correct, too... The grid lines angle in like you'd expect.